论文地址： DiffPool

Introduction

传统的GNN算法在Node-level的任务如节点分类、链路预测上有着较好的效果。但是，现有的GNN方法由于其存在平面化的局限性，因此无法学习图的层级表示（意味着无法预测整个图的标签），顾无法实现图分类任务。举个栗子，一个Graph，可以分成600个subgraph，每个节点都存在于其中的某个subgraph（一个节点只存在于一个subgraph中），每个subgraph拥有一个标签，如何预测subgraph的标签是这篇文章主要想解决的问题。传统的GNN的图分类方法都是为Graph中的所有节点生成Embedding，然后将对这些Embedding做全局聚合（池化），如简单的把属于同一个subgraph的节点求和或者输入到MLP中生成一个标签向量来表示整个subgraph，但是这样可能忽略的图的层级结构信息。

本文提出了一种端到端的可微可微图池化模块DiffPool，原理如下图所示：

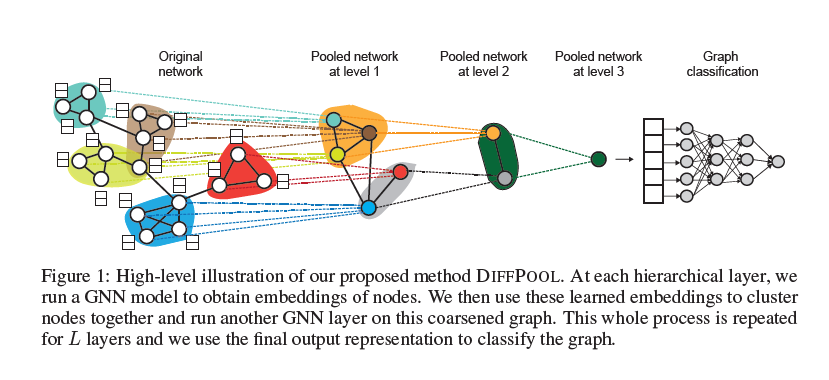
在深度GNN中的每层中为节点学习可微的软簇分配，将节点映射到簇中，这些簇作为新的节点作为下一层GNN的输入。上图的Original Network部分是一个Subgraph，传统的方法是直接求出这个Subgraph中每个节点的Embedding，然后相加或输入到一个神经网络中，得到一个预测向量，这种方法可以称为“全局池化”。DiffPool中，假设第$l$层的输入是$1000$个簇（如果是第一层输入就是1000个节点），我们先设置第$l+1$层需要输入的簇的个数（假设为$100$），也就是第$l$层输出的簇个数，然后在$l$层中通过一个分配矩阵将$1000$个簇做合并，合并成100个“节点”，然后将这100个节点输入到$l+1$层中，最后图中的节点数逐渐减少，最后，图中的节点只有一个，这个节点的embedding就是整个图的表示，然后将图输入到一个多层感知机MLP中，得到预测向量，在于真值的one-hot向量做cross-entropy，得到Loss。

Model：DiffPool

一个Graph表示为$\mathcal{G} = (A,F)$，其中$A \in {0,1}^{n \times n}$是Graph的邻接矩阵，$F \in \mathbb{R}^{n \times d}$表示节点特征矩阵，每个节点有$d$维的特征。给定一个带标签的子图集$\mathcal{D}=\left\{\left(G_{1}, y_{1}\right),\left(G_{2}, y_{2}\right), \ldots\right\}$， 其中 $y_{i} \in \mathcal{Y}$表示每个子图$G_i \in \mathcal{G}$的标签，任务目标是寻找映射$f: \mathcal{G} \rightarrow \mathcal{Y}$，将图映射到标签集。我们需要一个过程来将每个子图转化为一个有限维度的向量$\mathbb{R}^D$。

Graph Neural Networks

一般，GNN可以表示成"Message Passing"框架： $$ H^{(k)}=M\left(A, H^{(k-1)} ; \theta^{(k)}\right) $$ 其中$H^{(k)} \in \mathbb{R}^{n \times d}$表示GNN迭代$k$次后的node embedding，$M$是一个Message扩散函数，由邻接矩阵$A$和一个可训练的参数$\theta^{(k)}$决定。$H^{(k-1)}$是由前一个message passing过程生成的node embedding。当$k = 1$时，第一个GNN的输入为$H^{(0)}$是原始的节点特征$H^{(0)} = F$。

GNN的一个主要目标是设计一个Message Passage函数$M$，GCN（kipf.2016）是一种流行的GNN，$M$的实现方式是将线性变换和ReLU非线性激活结合起来: $$ H^{(k)}=M\left(A, H^{(k-1)} ; W^{(k)}\right)=\operatorname{ReLU}\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(k-1)} W^{(k-1)}\right) $$ 其中，$\tilde{A} = A+I$是一个加上自环的邻接矩阵，$\tilde{D}=\sum_{j} \tilde{A}_{i j}$是$\tilde{A}$的度矩阵，$W^{(k)} \in \mathbb{R}^{d \times d}$是一个可训练的权重矩阵，$W$与节点个数以及每个节点的度无关，可以看做一个特征增强矩阵，用来规定GCN的输出维度。

一个完整的GNN模型会迭代$K$次来输出最终的node embedding$Z = H^{(K)} \in \mathbb{R}^{n \times d}$。对于GCN，GAT，GraphSage，$K$一般取2-6。文中为了简单表示，忽略了GNN的内部结构，用$Z=GNN(A,X)$来表示一个任意的执行$K$次的GNN模块。

GNN和池化层的堆叠

这篇工作的目标是定义一个一般的，端到端的可微策略，允许以层级的方式堆叠多个GNN模块。给定原始的邻接矩阵$A \in \mathbb{R}^{n \times n}$，$Z=GNN(A,X)$十一GNN模块的输出（假设这个GNN模块做了3次迭代）。我们需要定义一个策略来输出一个新的粗化图，这个粗化图包含$m$个节点，$m < n$，它的邻接矩阵一个带权重的邻接矩阵$A’ \in \mathbb{R}^{m \times m}$，同时，输出node embedding $Z’ \in \mathbb{R}^{m \times d}$。这个粗化图（$m$个节点的图）作为下一层GNN的输入 （将$A’$和$Z’$输入下一个GNN层）。最后所有节点粗化为只有一个节点的图，这个节点的embedding就是这个subgraph的表示。因此，目标为：如何使用上一层GNN的输出结果，对节点做合并或池化，是的图中的节点减少，再将粗化的图输入到下一个GNN中。

基于可学习分配的可微分池化

DiffPool通过对一个GNN模块的输出学习一个聚类分配矩阵来解决这个问题。可微池化层根据$l-1$层的GNN模块（假设是一个3次迭代的GNN模块）产生的node embedding来对节点做合并，从而产生一个粗化图，这个粗化图作为$l$层GNN模块的输入，最终，整个subgraph被粗化为一个cluster，可以看做一个节点。

用分配矩阵进行池化

$S^{(l)} \in \mathbb{R}^{n_{l} \times n_{l+1}}$表示第$l$层的聚类分配矩阵，$S^{(l)}$的每一行表示第l层的每个节点（cluster）,每一列表示$l+1$层的每个cluster（节点）。$S^{(l)}_{ij}$表示第$l$层的节点$i$属于第$l+1$层cluster $j$的概率，所以$S^{(l)}$是个概率矩阵。

假如已经有了第$l$层的节点分配矩阵$S^{(l)}$，将第$l$层的邻接矩阵表示为$A^{(l)}$，将第$l$层GNN模块的输出节点特征（node embedding）表示为$Z^{(l)}$，通过DiffPool层可以将第$l$层的图粗化为$\left(A^{(l+1)}, X^{(l+1)}\right)=\operatorname{DIFFPOOL}\left(A^{(l)}, Z^{(l)}\right)$，其中，$A^{(l+1)}$是$l+1$层图的邻接矩阵，是一个粗化后的图，$X^{(l+1)}$是下一层的输入特征（node/cluster embedding）： $$ \begin{aligned} &X^{(l+1)}=S^{(l)^{T}} Z^{(l)} \in \mathbb{R}^{n_{l+1} \times d}\ &A^{(l+1)}=S^{(l)^{T}} A^{(l)} S^{(l)} \in \mathbb{R}^{n_{l+1} \times n_{l+1}} \end{aligned} $$ 上面第一个公式将第$l$层节点嵌入$Z^{(l)}$转化为下一层的输入特征$X^{(l+1)}$。第二个公式将第$l$层的邻接矩阵转化为$l+1$层的粗化图邻接矩阵$A^{(l+1)}$。$n_{l+1}$是$l+1$层节点（cluster）的数量。最后，将$A^{(l+1)}$和$X^{(l+1)}$作为下一层GNN的输入。这样图中的节点就由$n_l$个下降到$n_{l+1}$个。

学习分配矩阵S

第$l$层的输入特征$X^{(l)}$，用一个GNN模块（代码中是一个3层的GCN）得到node embedding： $$ Z^{(l)}=\mathrm{GNN}_{l, \text { embed }}\left(A^{(l)}, X^{(l)}\right) $$ 用另外一个GNN模块（代码中是一个3层的GCN）在用一个softmax转化为概率矩阵来的到节点分配矩阵： $$ S^{(l)}=\operatorname{softmax}\left(\mathrm{GNN}_{l, \mathrm{pool}}\left(A^{(l)}, X^{(l)}\right)\right) $$ $S^{(l)}$是一个$n_l \times n_{l+1}$的全链接矩阵，$S^{(l)}_{ij}$表示第$l$层的节点$i$属于第$l+1$层cluster $j$的概率。

$l=0$时，第一层GNN的输入是subgraph的原始邻接矩阵$A$和特征矩阵$F$，倒数第二层$l=L-1$时的分配矩阵$S^{(L-1)}$是一个全1向量，那么最后将所以节点归为一类，产生一个代表整个图的嵌入向量。

所以，把图节点的合并过程称为分层的图表示学习（Hierarchical Graph Representation Learning）。