论文地址:HTNE
Introduction
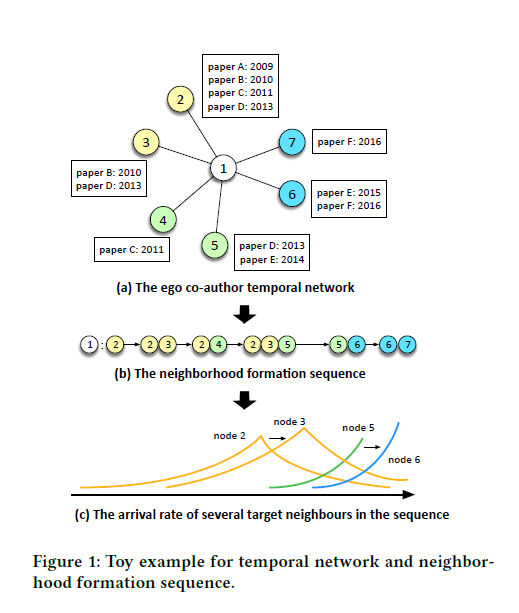
本文出发点在于捕获动态网络中节点和边的变化来在embedding中保持网络结构,举个简单的例子来说,如Fig. 1所示,是一个共同作者网络图。数字标注的节点是author,方框内是co-authored paper. 可以看到图中每个节点每条边加入网络中的时间是不同的。根据图中的信息,可以分析出例如前期1和2,3合作较紧密,后期转为了6,7。 并且(b)中所示,同一条边可能多次出现,这就比传统的单条边拥有更多语义信息。
另外,最近也有方法对动态网络的embedding做了研究,比如[29][30]的方法。但是他们的目的是将时间线分段为固定时间窗来对动态建模,但是这些方法依然没有考虑动态过程也就是网络随时序动态变化的信息。
因此,本文提出了基于霍克斯过程(Hawkes process)的时序网络表示学习方法,该方法是由序列事件驱动的(也就是序列的变化) 如Fig .1(b)所示 (b)图为节点1的邻域生成序列。霍克斯过程的思路是说历史上发生的事情对未来的概率密度函数有影响,只是随着时间流逝这种影响会逐渐减弱(Decay)。本文提出用霍克斯过程来捕获时间序列(也就是邻域生成序列)的激励效应。 尤其是历史事件对当前事件的影响。
通过把成对的向量映射到基本速率和历史影响,从而把低维向量被输入Hawkes过程。
另外历史邻居当前邻居的影响,不同节点是不同的,所以本文使用attention model来学习历史邻居对当前邻居影响的量化表示。
值得注意的是,本文目标是优化邻域生成序列的极大似然估计即条件强度函数(conditional intensity function)来邻域生成序列的到达率,而不是条件概率函数
Model
Definition
本文通过跟踪节点邻域的形成来捕获网络的形成过程。
Definition 1 : 时序网络 $G=(V,E,A)$, $A$ 是事件集, 边$(x,y) \in E$ 被表示为按时间顺序的时间序列,例如, $\mathbf{a}_{x,y}={a_1\to{a_2}\to{…}}\subset\mathcal{A}$, $a_i$ 表示时间$t_i$时刻的一个事件。
因此,网络中节点的相邻邻居可以根据与邻居的交互事件的时序被组织为序列,表示邻域形成过程。
Definition 2 : 对于给定节点$x$,邻域表示为$N(x)={y_i|i=1,2…}$.$x$的目标邻居到达事件可以表示为${x:(y_1,t_1)\to(y_2,t_2)\to…\to(y_n,t_n)}$,即邻域形成序列。每个元组表示在时间戳$t_i$时,$x$与$y_i$建立边。
Hawkes Process
点过程(Point Process)通过假设t时刻前的历史事件可以影响当前事件的发生,来对离散序列事件建模。
对于一个给定的节点$x \in V$, 在$x$的邻域生成序列中,到达目标邻居$y$的条件强度函数(或者可以说是$x$与$y$有边的可能性强度)可以表示为:
$$ \tilde{\lambda}_{y|x}(t)=\mu_{x,y}+\sum_{t_h<t}{\alpha_{h,y}\kappa(t-t_{h})}$$
其中,$\mu_{x,y}$表示构建一条连接节点$x$和$y$的基本率(base rate),$h$是t时刻前的历史目标节点,$\alpha_{h,y}$表示一个$t_h$时刻的历史目标节点$h$(该节点是$x$的邻居)对当前邻居$y$的影响强度。$\sum_{t_h<t}$表示遍历t时刻前$x$的所有邻居。$\kappa(t-t_{h})$表示随时间的衰减,可以表示成指数函数:
$$\kappa(t-t_h)=\exp(-\delta_s(t-t_h))$$
其中,减少率 $\delta$是一个源依赖参数,对于每一个源节点(每个序列的根),历史邻居对当前邻居形成的影响强度是不同的。具体来说,如果$\kappa$越大,说明$t_h$时刻的邻居对当前邻居的影响越大,即 $-\delta_s(t-t_h)$越大, $\delta_s(t-t_h)$越小,因为$t$是当前时刻的邻居,所以当$t_h$越接近当前邻居时刻时,$\kappa$越大,这就说明了里当前时刻之前越近的邻居,对当前时刻邻居的影响越大。
综上所述,$\kappa$的具体意义是随时间衰减的影响,其中$\delta_s$参数表示对于不同的源节点,影响是不同的。
如果$\tilde{\lambda}_{y|x}(t)$ 越大,说明x和y有边的可能性也越大。
直观的来看,基本率(base rate)$\mu_{x,y}$揭示了节点x和节点y之间的连接可能性。为了简洁,本文使用了**负平方欧式距离(negative squared Euclidean)**来反映表示向量间的相似度: $\mu_{x,y}=f(\mathbf{e}_x,\mathbf{e}_y)=-||\mathbf{e}_x-\mathbf{e}_y||^2$。同样的,在计算历史邻居$h$对当前邻居$y$的影响时,也采用这个方法,即: $\alpha_{h,y}=f(\mathbf{e}_h,\mathbf{e}_y)=-||\mathbf{e}_h-\mathbf{e}_y||^2$。
因为条件强度函数必须为正,所以使用如下公式: $\lambda_{y|x}(t)=\exp(\tilde\lambda_{y|x}(t))$。$exp()$对原函数进行了归一化,所以问题就转化为了given $x$, maximize likelihood: $p(y|x)$. 这就与传统的NE方法差不多了。。。
Attention
根据论文中(3)式,可以看出,$\sum_{t_h<t}{\alpha_{h,y}\kappa(t-t_{h})}$这一部分主要描述了历史邻居对当前邻居的影响,但是完全忽略了源节点$x$,因为源节点$x$的变化也会影响到历史邻居对当前邻居的亲近程度(affinity)。因此,本文引入了attention model。as follows:
$$w_{h,x} = \frac{\exp(-||\mathbf{e}_x-\mathbf{e}_h||^2)}{\sum_{h’}{\exp(-||\mathbf{e}_x-\mathbf{e}_{h’}||^2)}}$$
这是一个softmax函数 来根据源节点$x$的不同为它的邻居赋予不同权重。
最后, 历史邻居与当前邻居的连接紧密程度可以表示为: $$\alpha_{h,y}=w_{h,x}f(\mathbf{e}_h,\mathbf{e}_y)$$
Optimization
目标函数即为给定节点$x$以及基于邻域形成序列的霍克斯过程, 生成节点$y$的条件概率。 公式如下: $$p(y|x, \mathcal{H}_x(t)) = \frac{\lambda_{y|x}(t)}{\sum_{y’}{\lambda_{y’|x}(t)}}$$ 目标函数即为所有节点对的极大似然: $$\log \mathcal{L}=\sum_{x\in{\mathcal{V}}}{\sum_{y\in{\mathcal{H}_x}}}{\log{p(y|x,\mathcal{H}(t))}}$$
最后,由于softmax过程是calculating expensive,所以采用负采样优化损失函数。