目的:将图结构调整为适配LLM的输入。具体来说,将图节点表示为图结构感知和属性感知的序列,然后将序列映射到token embedding space中,从而使LLM可以用处理text tokens的方式来对Graph token embeddings进行处理。为了实现这个目标,就要求node sequence必须充分保存中心节点的结构信息。
Structure-Aware Graph Translation
LLaGA的目的是将graph翻译成可被LLM理解的token embedding sequence的形式。同时,这可以利用LLM固有的推理能力来处理图的任务,并且无需改变LLM的参数(foundation model)。为了实现这个目标,LLaGA将图结构转化为node embedding sequences,这些sequences融合了图的局部和更大范围的结构信息,然后将node embedding sequences通过一个projector转化为LLM可以处理的token embedding sequence。
第一步是将图转换为node embedding sequences。由于图分析的基本单位是节点,所以本工作开发了2个节点级templates,这些templates是多功能的,不仅可以用于节点级任务,也可以用于边级任务。分别是一个Neighborhood Detail Template,提供对中心节点及其周围环境的深入观察;Hop-Field Overview Template,提供了一个节点邻居的总结视角,可以拓展到更大的域。这两个模板都旨在编码节点周围的结构信息,为分析提供不同的视角。
Neighborhood Detail Template
Neighborhood Detail Template用于描述节点和其周围邻居的详细信息。给定一个中心节点 $v$,需要构造一个形状固定的tree。对于中心节点 $v$的每跳邻居,定义一组邻居采样的size: $n_1$, $n_2$, …,其中 $n_i$表示第 $i$跳邻居的采样数量。对于 $1$-hop邻居集合 $\mathcal{N}_v^1$,从其中随机采样 $n_1$个邻居,表示为 $\widetilde{\mathcal{N}}_v^1$。如果 $\left|\mathcal{N}_v^1\right|<n_1$,那么用placeholder nodes来补全 $n_1$个邻居。注意,这里定义的每跳邻居的采样数量 $n_1, n_2, \cdots$是应用于所有节点的。得到的 $v$-centered tree如下图所示:
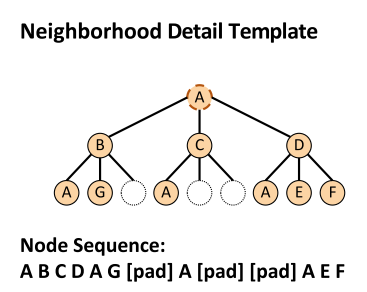
这里定义 $n_2 = 3$,如果2跳邻居不满3个节点,那么用 placeholder node $[\text{pad}]$来占位。然后我们从tree的中心节点开始遍历,可以把这棵计算树转换为一个固定长度的node sequence。这个node sequence描述了以 $A$为中心的局部邻域内的节点相对结构位置(从近到远)。
上面的步骤将中心节点和它的结构信息编码成一个节点序列,然后我们需要把这个节点序列映射到embedding space中。对于TAG(Text-Attributed Graph),使用现成的语言模型 $\phi$,例如SBERT,RoBERTa或SimTeG来编码文本信息,placeholder node的特征被编码为 $0$向量。然后进一步融合结构信息,每个节点在tree中的结构信息用Laplacian Embedding来表示,也就是拉普拉斯矩阵的特征向量在node id的位置来表示这个node在Tree中的结构信息,也就是相邻的节点有相似的embedding:
$$ L=I-\mathcal{D}^{-\frac{1}{2}} \mathcal{A}_{\text {tree }} \mathcal{D}^{-\frac{1}{2}}=U^T \Lambda U $$
其中 $U$的每行表示对应节点的Laplacian Embedding。注意到,我们预训练的时候,只需要计算一次Laplacian Embedding,以为对于任何图中的任何节点,都为它构造一样的computational tree,所以Laplacian Embedding是不变的。对于计算树induced node sequence $v_1, v_2, \cdots, v_n$,那么这个计算树中的节点 $v_i$的最终node embedding表示为:
$$ h_{v_i}= \begin{cases}\mathbf{0} || U_i, & \text { if } v_i=[p a d] ; \ \phi\left(x_{v_i}\right) || U_i, & \text { otherwise }\end{cases} $$
它结合了文本信息和节点与领域内其他节点的相对位置信息。
Hop-Field Overview Template
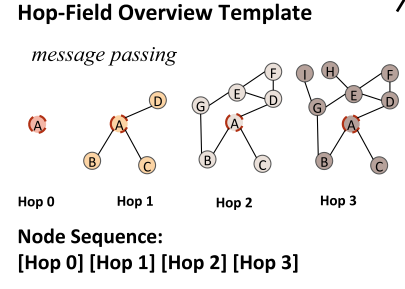
Hop-Field Overview Template提供的是一个关于中心节点和其邻居的总结视角。**Neighborhood Detail Template中sequence的每个元素是一个节点,Hop-Field Overview Template中每个元素是一跳节点的总结。**首先,用LM来初始话每个节点的特征,节点 $v$的初始特征为 $h_x^0=\phi\left(x_v\right)$。定义parameter-free message passing on encoded text features:
$$ h_v^i=\frac{1}{\left|\mathcal{N}_v^1\right|} \sum_{v^{\prime} \in \mathcal{N}_v^1} h_{v^{\prime}}^{i-1} $$
$h_v^1=\frac{1}{\left|\mathcal{N}_v^1\right|} \sum_{v^{\prime} \in \mathcal{N}_v^1} h_{v^{\prime}}^{0}$表示节点 $v$的 $1$-hop邻居的summarized embedding,即直接聚合邻居的原始特征。 $h_v^i$表示聚合邻居的 $i-1$阶特征,也就是 $v$的 $i$hop以内邻居的summarized embedding。那么可以依据中心节点和hop顺序关系构造一个序列 $h_v^1, h_v^2,\cdots$,用来表示中心节点和它的相对结构信息。这个方法牺牲了更多细节,但是保留了更广的感受野。
Mapping Node Embeddings into LLM’s token space
用于对齐节点的embedding space和LLM的token space,使得节点序列可以作为LLM的输入。定义一个可训练的projector $f_\theta$:
$$ e_i=f_\theta\left(h_i\right) $$
用来将序列中的每个节点embedding映射到token space。然后,node embedding sequence $h_1, h_2,\cdots, h_n$可以被转换成token embeddings $e_2, e_2,\cdots, e_n$。LLaGA中唯一的训练参数就是这个projector $f_\theta$。
Alignment Tuning
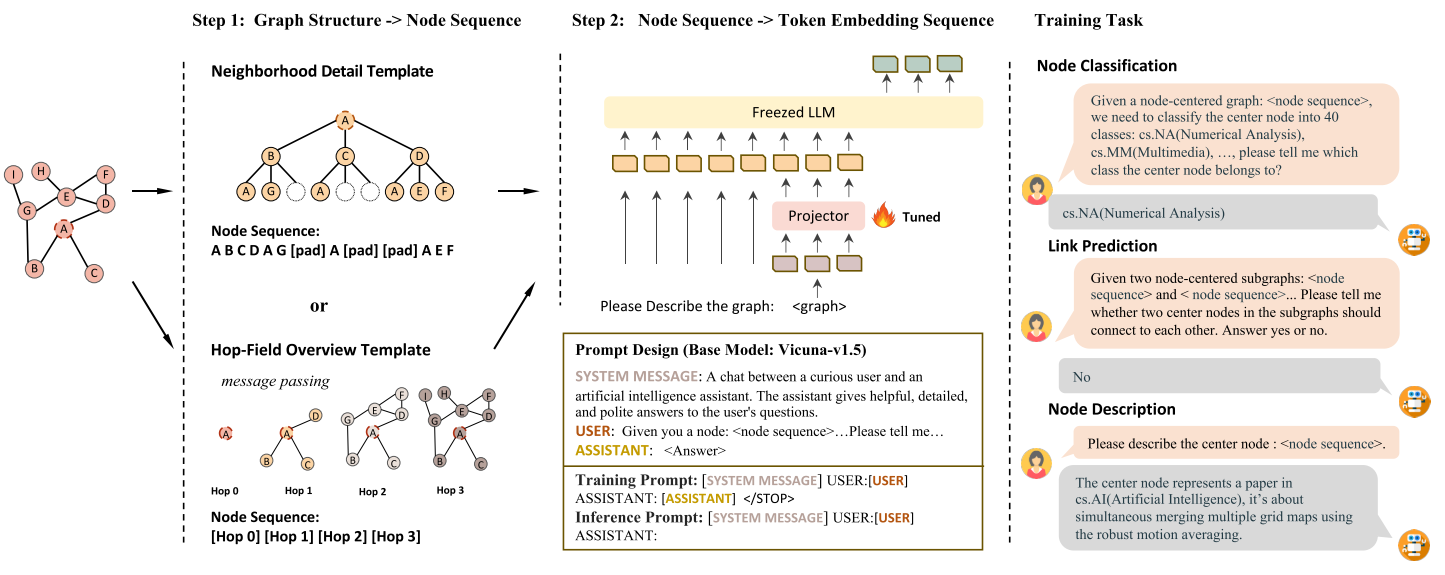
LLaGA采用3个预训练任务:节点分类,链路预测和节点描述(Node description)。其中,Node description任务用于将node embedding和特定文本描述对齐。这个特殊任务能够提供图的丰富语义解释,从而更深入地了解基于图的预测背后的逻辑。将这些预训练projector的任务统一成Questions and Answers的形式:
Questions: Please describe the center node: .
Answers: The center node represents a [paper / products /…], it’s about [node description].
在训练过程中,以chat的形式在组织问答,Vicuna-v1.5 (Chiang et al., 2023) 作为LLaGA的LLM模型。如上图step 2所示,在处理Freezed LLM的输入阶段,将SYSTEM MESSAGE,USER: [Give you a node] 都tokenize,然后将node sequence 替换为projected node embedding $e_1, e_2, \cdots$,然后将后面描述任务的prompt也tokenize,训练的优化目标是最大化生成正确答案的概率:
$$ \underset{\theta}{\operatorname{maximize}} \quad p\left(X_{\text {answer }} \mid X_{\text {graph }}, X_{\text {question }}, X_{\text {system }}\right) $$