论文地址： metapath2vec

Introduction

真实网络中通常包含多种类型的节点和关系，这些节点和关系共同组成了异质信息网络（Heterogeneous Information Network），传统的NE方法如DeepWalk, Line , node2vec更多关注与同质网络从而忽略了网络的异质性。针对这个问题，这篇文章提出了metapath2vec基于meta-path的随机游走来构建节点的异质邻域，采用异质Skip-gram模型来学习节点的representation。 另外，在负采样时也考虑异质性，从而进一步提出了metapath2vec++。如下：

Definition

Definition 1: 异质网络： $G = (V,E,T)$，其中每个节点和边分别对应一个映射 $\phi(v) : V \rightarrow T_{V}$ 和$\varphi(e) : E \rightarrow T_{E}$。 其中$T_V$和$T_E$分别表示节点的类型集合以及关系的类型集合。且$\left|T_{V}\right|+\left|T_{E}\right|>2$。

Definition 2: 异质网络表示学习 为网络中的节点学习一个$d$维的表示 $\mathrm{X} \in \mathbb{R}^{|V| \times d}$，$d \ll|V|$。节点的向量表示可以捕获节点间结构和语义关系。

Model

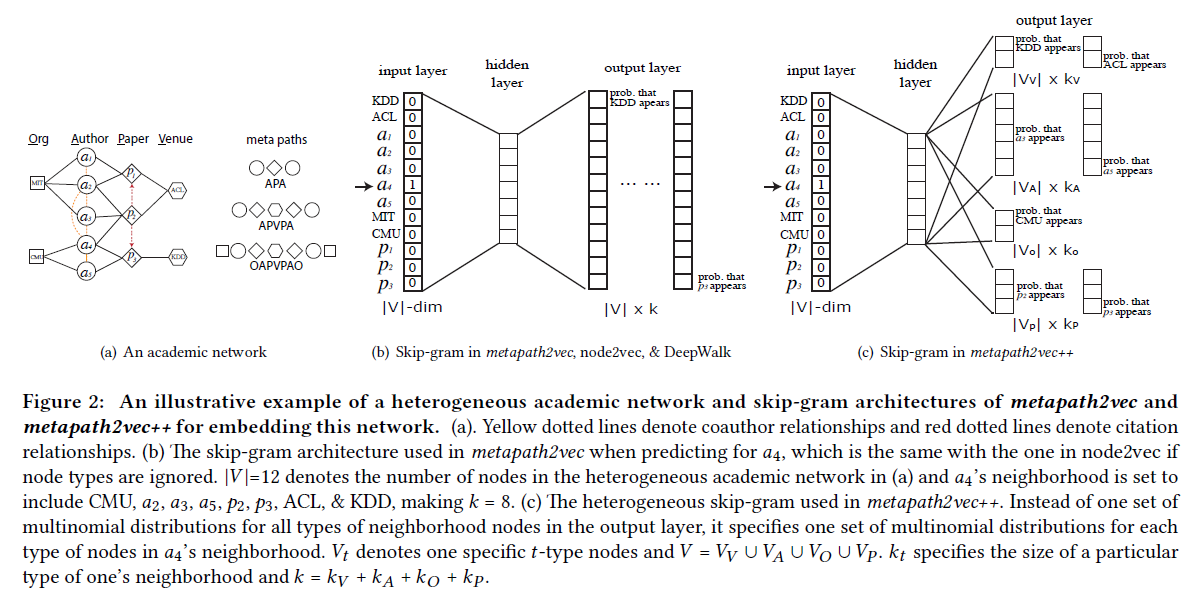
metapath2vec

Skip-Gram模型是给定一个节点，预测向下文节点的概率。metapath2vec的目的是考虑多种类型节点和多种类型关系的情况下，最大化网络概率。为了将异质信息融入skip-gram模型中，首先提出异质skip-gram。

Heterogeneous Skip-Gram

对于节点类型$|T_V| > 1$的网络$G$， 给定一个节点$v$，需要最大化属于类型$t \in T_V$的异质上下文节点的概率： $$ \arg \max_{\theta} \sum_{v \in V} \sum_{t \in T_{V}} \sum_{c_{t} \in N_{t}(v)} \log p\left(c_{t} | v ; \theta\right) $$ 其中，$N_t(v)$表示$v$属于第$t$个类型的邻居节点。 $p\left(c_{t} | v ; \theta\right)$ 表示给定节点$v$，它的$t$类型邻域概率： $p\left(c_{t} | v ; \theta\right)=\frac{e^{X_{c_{t}} \cdot X_{v}}}{\sum_{u \in V} e^{X_{u} \cdot X_{v}}}$，是一个softmax函数，$X_v$是节点$v$的表示。由于softmax函数的分母每一次都要遍历所有节点，所以采用负采样改进$\log p(\cdot)$ 如下： $$ \log \sigma\left(X_{c_{t}} \cdot X_{v}\right)+\sum_{m=1}^{M} \mathbb{E}_{u^{m} \sim P(u)}\left[\log \sigma\left(-X_{u^{m}} \cdot X_{v}\right)\right] $$ 其中 $\sigma(x)=\frac{1}{1+e^{-x}}$。

Meta-Path-Based Random Walks

在第$i$步时，转移概率$p(v^{i+1}|v^i)$表示为忽略节点类型情况下$v^i$的邻居分布。但是，PathSim提出，异质信息网络中的随机游走偏向于高度可见的节点，即具有主导数量路径的节点，所以 本文设计了基于元路径的随机游走来生成path，从而能够捕获不同类型节点间的结构联系和语义关系，提出了促进异构网络结构转换为metapath2vec的skip-gram。

一个meta-path模式$\mathcal{P}: V_{1} \stackrel{R_{1}}{\longrightarrow} V_{2} \stackrel{R_{2}}{\longrightarrow} \dots V_{t} \stackrel{R_{t}}{\longrightarrow} V_{t+1} \cdots \stackrel{R_{l-1}}{\longrightarrow} V_{l}$， 其中 $R=R_{1} \circ R_{2} \circ \cdots \circ R_{l-1}$ 节点类型$V_{1}$到$V_{l}$之间的组合关系。那么节点间的跳转概率定义为： $$ p\left(v^{i+1} | v_{t}^{i}, \mathcal{P}\right)=\left\{\begin{array}{cc}{\frac{1}{\left|N_{t+1}\left(v_{t}^{i}\right)\right|}} & {\left(v^{i+1}, v_{t}^{i}\right) \in E, \phi\left(v^{i+1}\right)=t+1} \\ {0} & {\left(v^{i+1}, v_{t}^{i}\right) \in E, \phi\left(v^{i+1}\right) \neq t+1} \\ {0} & {\left(v^{i+1}, v_{t}^{i}\right) \notin E}\end{array}\right. $$ 其中$v^i_t \in V_t$，$N_{t+1}\left(v_{t}^{i}\right)$表示属于$t$类型的节点$v$的属于$t+1$类型的邻居。如果下一个节点$v^{i+1}$和$v^i_t$之间有边，并且$v^{i+1}$是$t+1$类型的节点 那么转移概率服从平均分布。其中，$v^{i+1}$服从meta-path所定义的下移节点类型。如图（a）中，原路径为$OAPVPAO$，那么节点$a_4$的下一个节点必然要是$P$类。 由于meta-path的对称性，所以： $$ p\left(v^{i+1} | v_{t}^{i}\right)=p\left(v^{i+1} | v_{1}^{i}\right), \text { if } t=l $$

metapath2vec++

由于softmax做归一化时没有考虑节点类型，分母是对所有节点求和，所以为了融合节点类型，给出Heterogeneous negative sampling: $$ p\left(c_{t} | v ; \theta\right)=\frac{e^{X_{c_{t}} \cdot X_{v}}}{\sum_{u_{t} \in V_{t}} e^{X_{u_{t}} \cdot X_{v}}} $$ 如图（c）所示，metapath2vec++对每种类型节点指定不同的一组多项式分布，相当于在输出层根据节点类型，把异质网络分解成不同的同质网络，同样采用负采用的方法简化计算： $$ O(\mathrm{X})=\log \sigma\left(X_{c_{t}} \cdot X_{v}\right)+\sum_{m=1}^{M} \mathbb{E}_{u_{t}^{m} \sim P_{t}\left(u_{t}\right)}\left[\log \sigma\left(-X_{u_{t}^{m}} \cdot X_{v}\right)\right] $$ 算法如下：