单一状态Monte Carlo规划:多臂赌博机(Multi-armed bandits)
单一状态$s$, $k$种action($k$个摇臂)。
在摇臂赌博机问题中,$s$每次以随机采样形式采取一种行动$a$。 例如,随机拉动第$k$个赌博机,得到的reward为$R(s, a_k)$。问下一次拉动哪个赌博机,才能获得最大Reward?
多臂赌博机问题是一种序列决策问题,这种问题需要在利用(exploitation)和探索(exploration)之间保持平衡。
利用(Exploitation): 保证在过去决策中得到最佳回报
探索(Exploration):寄希望在未来能够得到更大的汇报
例如, $s$摇动10次赌博机,其中第5次获得最大回报,那么下一次摇动赌博机可能选第5个赌博机,即“利用”(根据过去的最佳回报来施展下一次行为),第11次摇动的action为$a_5$。
但是摇动10次后,可能有的赌博机尚未摇动,未摇动的赌博机可能会有更大回报,即“探索”。
悔值函数
如果有$k$个赌博机, 这$k$个赌博机产生的操作序列为$X_{i,1}, X_{i,2}, \cdots (i = 1,\cdots, k)$。 在时刻$t=1,2,\cdots$, 选择第$I_t$个赌博机后,可得到的奖励为$X_{I_t,t}$, 则在$n$次操作$I_1,\cdots,I_n$后,可如下定义悔值函数: $$ R_n = \max_{i=1,\cdots,k} \sum^n_{t = 1} X_{i,t}-\sum^n_{t=1}X_{I_t, t} $$ $i$: 第$i$个赌博机
$I_t$: $t$时刻选择的赌博机
$\max_{i=1,\cdots,k} \sum^n_{t = 1} X_{i,t}$: 最理想(大)的奖励
$X_{I_t, t}$: $t$时刻选择赌博机$I_t$的reward
$\sum^n_{t=1}X_{I_t, t}$: $n$次选择的总奖励。
$R_n$越大,就代表$n$次决策的结果越差。
上置信区间(Upper Confidence Bound, UCB)
UCB旨在探索和利用间去的平衡
在UCB方法中,使$X_{i, T_{i}(t-1)}$ 来记录第$i$个赌博机在过去$t-1$时刻内的平均奖励,则在第$t$时刻,选择使如下具有最佳上限置信区间的赌博机: $$ I_{t}=\max_{i \in{1, \ldots, k}}\left\{\overline{X_{i, T_{i}(t-1)}}+C_{t-1, T_{i}(t-1)} \right\}. $$ 其中$I_{t}$为$t$时刻要摇的赌博机,
$\overline{X_{i, T_{i}(t-1)}}$要尽可能大:为$t$时刻之前赌博机$i$的平均reward 要尽可能大,
$C_{t-1, T_{i}(t-1)}$要尽可能小:$t$时刻之前$i$出现的次数要尽可能少
其中$C_{t,T_i(t)}$的取值定义如下: $$ C_{t,T_i(t)}=\sqrt{\frac{2 \operatorname{In} t}{T_i(t)}} $$ 其中$T_i(t)$表示 $t$时刻以前(包括$t$),选到赌博机$i$的次数总和。
若赌博机在$t$时刻之前(包括$t$)时刻摇动的次数越少,$C_{t,T_i(t)}$越大
选出的$I_t$要满足在$t$之前的平均reward尽可能大(利用), 且在$t$之前出现次数尽可能少(探索)。
也就是说,在第时刻,UCB算法一般会选择具有如下最大值的第$j$个赌博机: $$ \begin{aligned} U C B&=\bar{X}_{j}+\sqrt{\frac{2 \operatorname{Inn}}{n_{j}}} \text { 或者 } U C B=\bar{X}_{j}+C \times \sqrt{\frac{2 \operatorname{In} n}{n_{j}}} \\ I_t &= \mathrm{argmax}_j UCB(j) \end{aligned} $$ 其中$\bar{X}_{j}$是第$j$个赌博机在过去时间内所获得的平均奖赏值,$n_j$是在过去时间内拉动第$j$个赌博机臂膀的总次数,$n$是过去时间内拉动所有赌博机臂膀的总次数。$C$是一个平衡因子,其决定着在选择时偏重探索还是利用。
从这里可看出UCB算法如何在探索-利用(exploration-exploitation)之间寻找平衡:既需要拉动在过去时间内获得最大平均奖赏的赌博机,又希望去选择拉动臂膀次数最少的赌博机。
Monte Carlo Tree Search
MCTS has four step:
- Selection 选择
- Expansion 拓展
- Simulation(rollout) 模拟
- Backpropagation 回溯

选择
从根节点R开始,向下递归选择子节点,直至选择一个叶子节点L。 具体来说,通常用UCBl(Upper Confidence Bound,上限置信区间)选择最具“潜力”的后续节点: $$ U C B=\bar{X}_{j}+\sqrt{\frac{2 \operatorname{In} n}{n_{j}}} $$
拓展
如果L不是一个终止节点(即博弈游戏不),则随机创建其后的一个未被访问节点,选择该节点作为后续子节点C。
模拟
从节点C出发,对游戏进行模拟,直到博弈游戏结束。
反向传播
用模拟所得结果来回溯更新导致这个结果的每个节点中获胜次数和访问次数。
包含两种策略学习机制:
搜索树策略:从已有的搜索树中选择或创建一个叶子结点(即蒙特卡洛中选择和拓展两个步骤).搜索树策略需要在利用和探索之间保持平衡。
模拟策略:从非叶子结点出发模拟游戏,得到游戏仿真结果。
例子: 围棋
以围棋为例,假设根节点是执黑棋方。
图中每一个节点都代表一个局面,每一个局面记录两个值A/B
A: 该局面被访问中黑棋胜利次数。对于黑棋表示己方胜利次数,对于白棋表示己方失败次数(对方胜利次数);
B: 该局面被访问的总次数
初始状态:
根节点(12/21)是当前局面,该局面被访问过21次,其中黑棋访问该局面后最终获胜12次。 黑执棋方遇到该局面(根节点局面)开始选择下一步action。
选择
黑执棋方遇到(12/21)这个局面时有3个有效action, 黑执行这三个action会得到3种局面(7/10),(5/8), (0/3). 黑执棋方要选择其中一个action,是的棋局变为这三种中的一种,那么要如何选择action呢?我们先分别计算UCB1:
左一: 7/10对应的局面Reward为: $$ \frac{7}{10} + \sqrt{\frac{\log (21)}{10}} = 1.252 $$ 3中局面共21次被模拟到,其中,该局面被访问过10次(探索, 第二项), 黑棋遇到该局面后最终获胜7次(利用, 第一项)。
左二:(5/8)对应局面Reward: $$ \frac{5}{8} + \sqrt{\frac{\log(21)}{8}} = 1.243 $$ 左三: (0/3)对应局面Reward: $$ \frac{0}{3} + \sqrt{\frac{\log(21)}{3}} = 1.007 $$ 由此可见,黑棋选择会导致局面(7/10)的action进行走琪。

白棋遇到局面(7/10)时,有两个有效的action, 分别会导致局面A/B = 2/4和5/6, A为白棋访问该局面后失败的次数,所以白棋访问该局面最终胜利的次数应该是$B-A$:
左一: (2/4)对应的局面Reward (白棋尽可能获胜)为: $$ (1-\frac{2}{4}) + \sqrt{\frac{\log(21)}{4}}=1.372 $$ 左二: (5/6)对应的局面Reward为: $$ (1-\frac{5}{6}) + \sqrt{\frac{\log(21)}{4}}=0.879 $$ 因此白棋会选择(2/4)局面
即每一步都寻找最佳应对方式,来最终评估更节点局面的好坏

白色执棋方选择action后到达局面(2/4), 黑棋执棋方面对该局面,有两种action可选,分别会到达(1/3)和(1/1), 分别计算UCB1 得:
左一: (1/3)对应reward 为: $$ \frac{1}{3} + \sqrt{\frac{\log (21)}{3}} = 1.341 $$ 左二:(1/1)对应reward为: $$ \frac{1}{1} + \sqrt{\frac{\log (21)}{1}} = 2.745 $$ 则黑棋选择action 使得局面变为(1/1)。右图中可见(1/1)为叶子节点, 白棋面对该局面暂时无候选局面(action),则进入下一个步骤,拓展。
拓展

白棋执棋方面对局面(1/1),因为已经是叶子节点, 所以(1/1)会随机产生一个未被访问过的新节点,初始化为(0/0),接着在该节点下进行模拟。 进入第三部, 模拟。
模拟
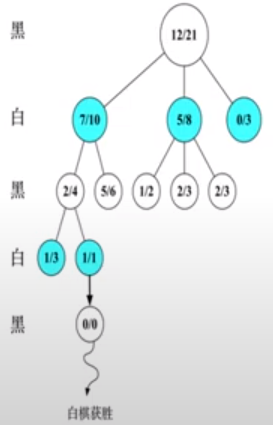
黑棋执棋方面局面(0/0),开始进行游戏仿真, 假设经过一些列仿真后,最终白棋获胜,即从更节点到最终模拟结束的叶子节点黑棋失败了。 进入第四部,回溯
回溯
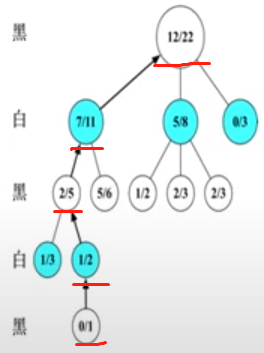
根据仿真结果来更新该仿真路径上的每个节点的A/B值。 因为该次模拟最终白棋获胜,所以向上回溯路径上的所有父节点,父节点的A不变,B+1。 若最终黑棋获胜,则父节点的A+1, B+1。
在有限时间里, MCTS会不断重复4个步骤,所有节点的A,B 值会不断变化
到某个局面(节点)后如何下棋(action), 会选择所有有效Action中UCB1值最大的节点,作为下棋的下一步。