Introduction

本文旨在通过多视图Contrastive Learning 来学习节点表示和图表示。其中对比视图为结构视图（structural view）。本文发现，两个以上的对比视图不会提升性能（我觉得仅是针对本文的Diffusion-based view吧~）。本文实验性的表明了基于一阶邻居和图扩散视图做CL可以达到最好的效果。

为了将对比学习应用到图表示学习任务，本文提出通过最大化图的不同结构视角的互信息来作为监督信号。通过对提出框架的系统研究，本文展示了一些GCL和visual CL上的不同：（1）将view数量（即增强）增加到两个以上不会提高性能，最好的性能是通过对比来自一阶邻居view的embedding和graph diffusion的embedding，(2) 与对比图编码或多尺度编码相比，跨视图对比节点和图编码在node classification 和 graph classification上都能获得更好的结果。 (3) 与分层图池化方法（例如DiffPool相比）一个简单的Readout在这node classification 和 graph classification上实现了更好的性能，以及 (4) 应用正则化（early stopping除外）或归一化层对性能有负面影响。

Method

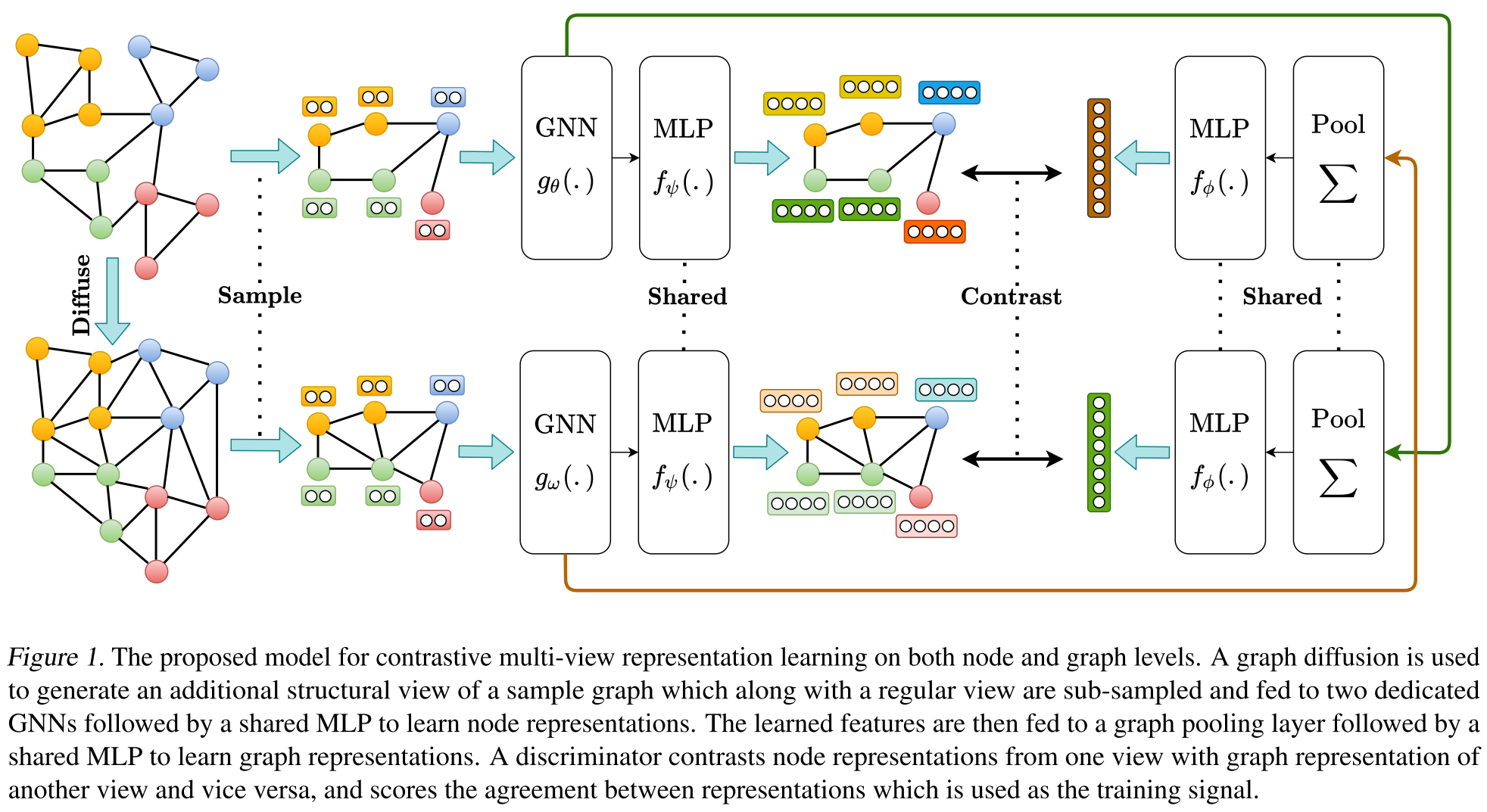
MVGRL通过最大化一个view的node embedding和另一个view的graph embedding之间的互信息来学习节点和图表示。如上图所示，MVGRL由以下几个部分构成

增强机制：将样本图转化为同一个图的相关view，这个view只是structural view，不会改变原图中的node feature，然后对两个增强图中的相同节点（identical node）进行子采样，类似于CV中的域剪裁。
两个专用的GNNs，每个view一个GNN，再接一个共享的MLP作为projection head，来为两个view学习representation。
图池化层，在MLP后学习两个图的graph-level representation。
判别器 来对比一个图的embedding和另一个图的节点embedding,并对他们的一致性（agreement）评分。

Augmentations

考虑两种类型的图增强：(1) 对初始节点特征进行操作的特征空间增强，例如，mask或添加高斯噪声，以及 (2) 通过添加或删除连通性、子采样或使用最短路径或diffusion matrix生成全局视图来对做图结构增强。前一种增强可能是有问题的，因为许多数据集不带有初始节点特征。此外，观察到在任一空间上屏蔽或添加噪声都会降低性能。因此，本文选择生成全局视图，然后进行子采样。

实验表明，在大多数情况下，最好的结果是通过将邻接矩阵转化为扩散矩阵，并将这两个矩阵视为同一图的结构的两个一致view。因为邻接矩阵和扩散矩阵分别提供了图结构的局部和全局视图，从这两种view中学习到的表示之间最大一致性，从而鼓励模型同时编码的局部和全局信息。

Diffusion matrix从全局角度提供了任意节点对之间的相关性，其中$\mathbf{T} \in \mathbb{R}^{n \times n}$是通用转移矩阵，$\Theta$是权重系数，决定了全局和局部信息的比例，即对于每个节点，不同层次信息的比重， $\Theta_{k}$越大，表示全局信息权重越大。令$\sum_{k=0}^{\infty} \theta_{k}=1, \theta_{k} \in[0,1]$，$\lambda_{i} \in[0,1]$,其中$\lambda$是$\mathbf{T}$的特征向量，这样来保证$\mathbf{S}$可以收敛到一个固定矩阵。扩散用快速近似值和稀疏化方法计算： $$ \mathbf{S}=\sum_{k=0}^{\infty} \Theta_{k} \mathbf{T}^{k} \in \mathbb{R}^{n \times n} $$ 给定一个邻接矩阵$\mathbf{A} \in \mathbb{R}^{n \times n}$和一个对角度矩阵$\mathbf{D} \in \mathbb{R}^{n \times n}$, Personalized PageRank (PPR)和Heat Kernel分别为两种不同的Diffusion matrix实例。对于PPR和HK，转移概率矩阵定义为$\mathbf{T}=\mathbf{A} \mathbf{D}^{-1}$。PPR将第$k$层的权重系数设置为$\theta_{k}=\alpha(1-\alpha)^{k}$, 而HK将第$k$层的权重系数设置为$\theta_{k}=e^{-t} t^{k} / k !$。

PPR的封闭阶如下所示： $$ \mathbf{S}^{\mathrm{PPR}}=\alpha\left(\mathbf{I}_{n}-(1-\alpha) \mathbf{D}^{-1 / 2} \mathbf{A} \mathbf{D}^{-1 / 2}\right)^{-1} $$ HK的封闭解如下所示： $$ \mathbf{S}^{\text {heat }}=\exp \left(t \mathbf{A} \mathbf{D}^{-1}-t\right) $$

Sub-Sampling

从一个view中随机采样节点及其边，并从另一个view中选择exact的的节点和边 (如示意图所示，从第一个图中采样节点和边的子图作为一个view，从第二个图中采样相同节点以及这些节点之间的边作为另一个view，来做对比学习)。这个过程允许MVGRL应用于具有图数据不适合GPU内存的inductive任务，也可以通过将子样本视为独立的图来考虑transductive任务。

Encoder

和其他GCL方法不同的是，这里不同视图使用的是各自的GNN编码器，邻接矩阵和Diffusion matrix是同一个图的两个一致视角，分别反映了局部和全局性质。首先，为两种view采样之后的子图分别定义GNN encoder：$g_{\theta}(.), g_{\omega}(.): \mathbb{R}^{n \times d_{x}} \times \mathbb{R}^{n \times n} \longmapsto \mathbb{R}^{n \times d_{h}}$，使用最简单的GCN，传播矩阵分别为normalized adjacency matrix $\sigma(\tilde{\mathbf{A} }X \boldsymbol{\Theta})$ 和 Diffusion Matrix: $\sigma(\mathbf{S} X \boldsymbol{\Theta})$。学习到的embedding输入projection head （MLP）$f_{\psi}(.): \mathbb{R}^{n \times d_{h}} \longmapsto \mathbb{R}^{n \times d_{h}}$中，得到两个view的输出node embedding matrix: $\mathbf{H}^{\alpha}, \mathbf{H}^{\beta} \in \mathbb{R}^{n \times d_{h}}$。

接下来使用pooling $\mathcal{P}(.): \mathbb{R}^{n \times d_{h}} \longmapsto \mathbb{R}^{d_{h}}$ 输出两个view的graph representations。本文采用JKnet中的跳连机制，即GNN的每层输出做sum pooling, 然后将所有层拼起来做特征变换： $$ \vec{h}_{g}=\sigma\left(||_{l=1}^{L}\left[\sum_{i=1}^{n} \vec{h}_{i}^{(l)}\right] \mathbf{W}\right) \in \mathbb{R}^{h_{d}} $$ 其中$\vec{h}_{i}^{(l)}$是节点$i$的第$l$层输出，$||$是concatenation， $\mathbf{W} \in \mathbb{R}^{\left(L \times d_{h}\right) \times d_{h}}$是特征变换参数，$\sigma$是PReLU非线性激活。最终，将图表示输入到一个projection head $f_{\phi}(.): \mathbb{R}^{d_{h}} \longmapsto \mathbb{R}^{d_{h}}$ 中，得到最终的图表示：$\vec{h}_{g}^{\alpha}, \vec{h}_{g}^{\beta} \in \mathbb{R}^{d_{h}}$。

在推理阶段，由于两个view来自同一个图，可以把两个view的表示结合起来作为原图的表示：两个view的graph embedding直接相加，作为原图 embedding.。两个view的node embedding 直接相加，作为原图的node embedding $\vec{h}=\vec{h}_{g}^{\alpha}+\vec{h}_{g}^{\beta} \in \mathbb{R}^{n}$ 。 $\mathbf{H}=\mathbf{H}^{\alpha}+\mathbf{H}^{\beta} \in \mathbb{R}^{n \times d_{h}}$。这里得到的原图embedding可以应用于下游任务。

Training

为了端到端训练encoder并学习与下游任务无关的丰富节点和图级表示，本文利用 Deep InfoMax 方法并通过对比一个视图的节点表示与图表示来最大化两个视图之间的互信息。实验表明，这种方法在节点和图分类上始终优于对比图-图或多尺度编码。目标定义如下： $$ \max_{\theta, \omega, \phi, \psi} \frac{1}{|\mathcal{G}|} \sum_{g \in \mathcal{G}}\left[\frac{1}{|g|} \sum_{i=1}^{|g|}\left[\operatorname{MI}\left(\vec{h}_{i}^{\alpha}, \vec{h}_{g}^{\beta}\right)+\operatorname{MI}\left(\vec{h}_{i}^{\beta}, \vec{h}_{g}^{\alpha}\right)\right]\right] $$ 其中$\theta, \omega, \phi, \psi$为是GNN encoder和projection head的参数, $|\mathcal{G}|$是图数量，$|\mathcal{g}|$是图中节点数， $\vec{h}_{i}^{\alpha}, \vec{h}_{g}^{\beta}$分别表示view $\alpha$中的节点$i$的representation，和view $\beta$的 graph representation。

互信息判别器： $\mathcal{D}(., .): \mathbb{R}^{d_{h}} \times \mathbb{R}^{d_{h}} \longmapsto \mathbb{R}$简单的设置为表示向量间的内积相似度： $$ \mathcal{D}\left(\vec{h}_{n}, \vec{h}_{g}\right)=\vec{h}_{n} \cdot \vec{h}_{g}^{T} $$ 作者发现当判别器和projection head集成到双线性层中时，节点分类基准略有改进。为了确定 MI 估计器，实验中调查了四个估计器并为每个基准选择了最好的一个。

正样本采样自联合分布$x_{p} \sim p\left(\left[\mathbf{X}, \tau_{\alpha}(\mathbf{A})\right],\left[\mathbf{X}, \tau_{\beta}(\mathbf{A})\right]\right)$，从边际乘积中采样负样本 $x_{p} \sim p\left(\left[\mathbf{X}, \tau_{\alpha}(\mathbf{A})\right]\right) p\left(\left[\mathbf{X}, \tau_{\beta}(\mathbf{A})\right]\right)$。利用小批量随机梯度下降法对模型参数进行优化。 MVGRL算法如下：

Introduction#

Method#

Augmentations#

Sub-Sampling#

Encoder#

Training#