Introduction
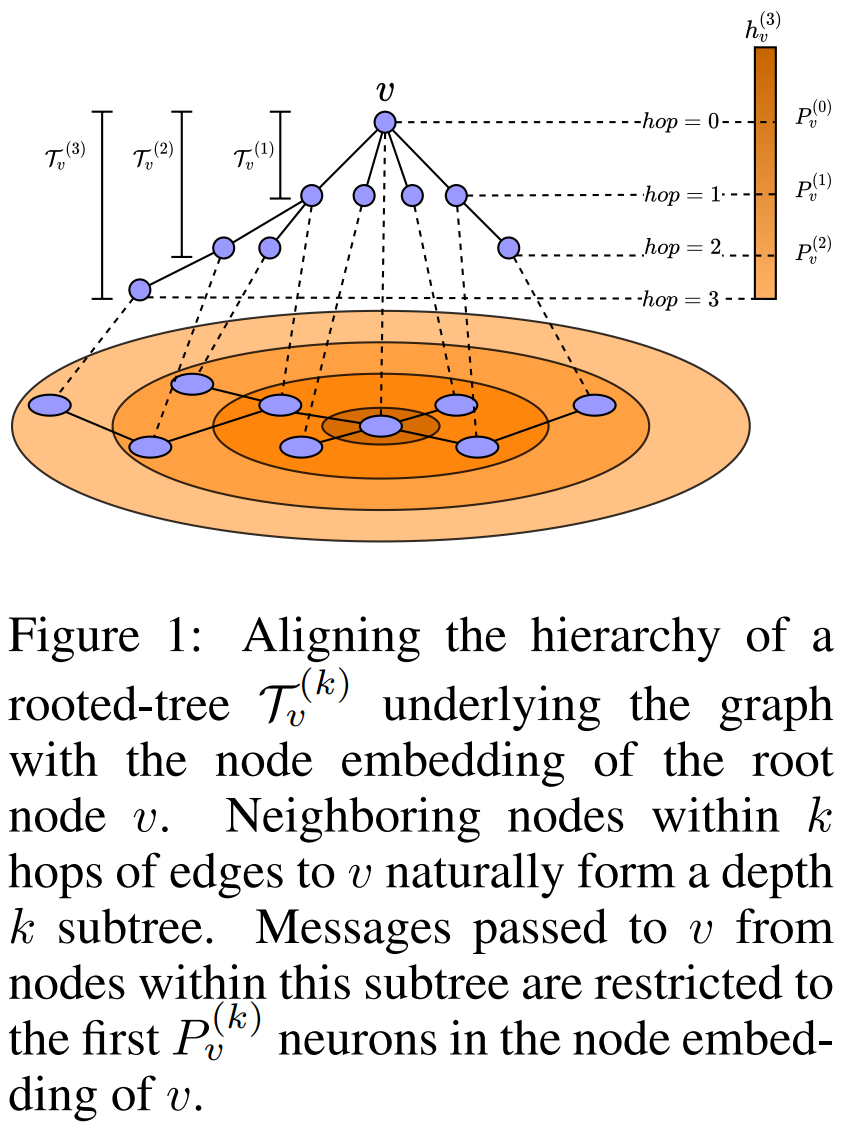
多层message passing后,GNN会导致Over-smoothing使得节点表示趋同。另一方面,标签不同的相邻节点特征会混合,导致不同标签节点边的难以区分,即Heterophily问题。在本文中,提出对传递到节点的message进行排序,即表示向量的特定neuron块编码特定hop的消息。通过将节点rooted computation tree的层次和表示向量neuron 块对齐。如下图所示,3层GNN对节点$v$的输出$h_v^{(3)}$的前$P_v^{(0)}$个neurons 编码1 hop邻居信息,$[P_v^{(0)}, P_v^{(1)}]$编码了第1层另据的信息。通过以确定的顺序编码邻居信息,来避免hops的特征融合,即一个节点的embedding的神经元要和计算书的层次对齐,不同层分配不同的neuron。也就是按照顺序将不同层的邻居信息编码到最终表示$h_v^{(k)}$的不同维度区间中。
Approach
Aligning Rooted-Tree with Node Embedding
对于一个节点$v$,显然它的第$k-1$层rooted-tree $\mathcal{T}^{(k-1)}_v$是$k$层rooted-tree $\mathcal{T}^{(k)}_v$的子树: $$ \mathcal{T}_v^{(0)} \subseteq \mathcal{T}_v^{(1)} \subseteq \cdots \subseteq \mathcal{T}_v^{(k)} \subseteq \cdots \subseteq \mathcal{T}_v^{(K)} $$ 随着$k$的增加,$\mathcal{T}_v^{(K)}$会变得越来越大且复杂,且包含之前层的所有信息。所以$\mathcal{T}_v^{(K)}$需要更多neuron (最终表示向量$h_v^{(k)}$中的维度) 来编码信息。由于$\mathcal{T}_v^{(k-1)}$是$\mathcal{T}_v^{(k)}$的子树,所以在表示向量$h_v^{(k)}$中,编码tree $\mathcal{T}_v^{(k)}$信息的neurons要包含编码 tree$\mathcal{T}_v^{(k-1)}$信息的neurons。具体来说,关于节点$v$的$k-1$层rooted-tree $\mathcal{T}_v^{(k-1)}$,它的信息会被编码到$h_v^{(K)}$的前$P_v^{(k-1)}$个neuron中(维度),对于下一个层次的rooted-tree $\mathcal{T}_v^{(k)}$,它会被编码到$h_v^{(K)}$的前$P_v^{(k)}$个neuron(维度)中。因为$\mathcal{T}_v^{(k-1)}$是$\mathcal{T}_v^{(k)}$的子树,所以$P_v^{(k-1)} \leq P_v^{(k)}$。 $v$的$K$层最终表示$h_v^{(K)}$,它的每个维度是一个neuron,前$P_v^{(k-1)}$个neurons编码了前$k-1$ hop邻居的信息,前$P_v^{(k)}$个neurons编码了前$k$ hop邻居的信息, 在两个分割点$P_v^{(k-1)}$和$P_v^{(k)}$之间的neurons要编码的是第$k$ hop邻居的信息。所以节点$v$在$K$层GNN下的最终embedding$h_v^{(K)} \in \mathbb{R}^D$ 会被$K+1$个分割点分成$K+1$块,其中前$P_v^{(0)}$个neurons编码的是节点$v$的自身信息,$P_v^{(k)}$为$h_v^{(K)}$的split point,且: $$ P_v^{(0)} \leq P_v^{(1)} \leq \cdots \leq P_v^{(k)} \leq \cdots \leq P_v^{(K)} = D $$
The Split Point
分割点$P_v^{(k)}$是一个index,会将$D$维node embedding 分为2块,$[0, P_v^{(k)}-1]$的neurons编码了前$k$层邻居的信息。 定义一个$D$维gating向量$g^{(k)}_v = [1,1,1,1,1,1,0,0,0,0,0]$其中前$P_v^{(k)}$个entries是1, 后面为0,即筛选出前$k$层要编码进的neurons: $$ h_v^{(k)}=g_v^{(k)} \circ h_v^{(k-1)}+\left(1-g_v^{(k)}\right) \circ m_v^{(k)} $$ 其中第$k$层的信息$h_v^{(k-1)}$保留在第$k+1$层embedding $h_v^{(k)}$的前$P_v^{(k)}$个neuron中,而$h_v^{(k)}$的后面部分neuron编码新聚合的邻居信息,通过这种方式,将每一个hop的信息分开。 再下一层时, $h_v^{(k)}$的信息就会被编码到$D$个neurons中的前$P_v^{(k+1)}$个neuron中,那么其实$P_v^{(k)}$到$P_v^{(k+1)}$之间的neuron实际上只包含了$m_v^{(k)}$的信息,即第$k$个hop的信息。以这种方式将每一个hop的邻居信息按顺序编码到最终表示向量$h_v^{(K)}$中。
然而binary gating vector $g^{(k)}_v$ 来自于离散操作,导致$g^{(k)}_v$的学习不可微,使得每个hop用多少神经元来保存不可自适应学习。 为了解决该问题,将$g^{(k)}_v$定义为关于root node $h_v^{(k-1)}$和messge $m_v^{(k)}$ 的函数,$g_v^{(k)}$的split point $P_v^{(k)}$分割了前面所有层的信息和第$k$ hop的邻居信息,这里将$\hat{g}_v^{(k)}$定义为一个从右向左的累加向量: $$ \hat{g}_v^{(k)}=\operatorname{cumax}_{\leftarrow}\left(f_{\xi}^{(k)}\left(h_v^{(k-1)}, m_v^{(k)}\right)\right)=\operatorname{cumax}_{\leftarrow}\left(W^{(k)}\left[h_v^{(k-1)} ; m_v^{(k)}\right]+b^{(k)}\right) $$ 进一步 由于$\hat{g}_v^{(k)}$是可学习的,它的split point为$P_v^{(k)}$ , 因此并不能保证$\hat{g}_v^{(k+1)}$的split point $P_v^{(k+1)}$会相对于$P_v^{(k)}$右移,因此本文提出了可微OR操作来确保$P_v^{(k+1)}\geq P_v^{(k)}$: $$ \tilde{g}_v^{(k)}=\operatorname{SOFTOR}\left(\tilde{g}_v^{(k-1)}, \hat{g}_v^{(k)}\right)=\tilde{g}_v^{(k-1)}+\left(1-\tilde{g}_v^{(k-1)}\right) \circ \hat{g}_v^{(k)} $$
Putting it All Together
Ordered GNN的第$k$层message passing如下:
首先计算第$k$hop邻居的message: $$ m_v^{(k)}=\operatorname{MEAN}\left(\left\{h_u^{(k-1)}: u \in \mathcal{N}(v)\right\}\right) $$ 计算当前层的split point $P_v^{(k)}$和门控向量$\tilde{g}_v^{(k)}$: $$ \begin{aligned} & \hat{g}_v^{(k)}=\operatorname{cumax}_{\leftarrow}\left(f_{\xi}^{(k)}\left(h_v^{(k-1)}, m_v^{(k)}\right)\right) \ & \tilde{g}_v^{(k)}=\operatorname{SOFTOR}\left(\tilde{g}_v^{(k-1)}, \hat{g}_v^{(k)}\right) \end{aligned} $$ 利用门控向量分块聚合当前节点embedding和新加入的hop信息: $$ h_v^{(k)}=\tilde{g}_v^{(k)} \circ h_v^{(k-1)}+\left(1-\tilde{g}_v^{(k)}\right) \circ m_v^{(k)} $$